Fórmula Básica da Probabilidade.

Fórmula Básica da Probabilidade de ocorrer um Evento.

Pascal descreveu a fórmula da probabilidade de um evento E como sendo:

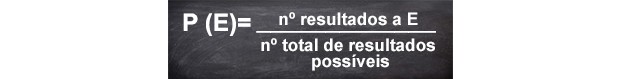
Traduzindo a fórmula, a probabilidade de um evento ocorrer é o numero de casos favoráveis dividido pelo numero de casos possíveis.

Veja um exemplo simples: Uma moeda “honesta” é lançada. 
Qual é a probabilidade de sair 1 cara ou 1 coroa?

Representamos um espaço amostral, pela letra S, esse é o total de 
casos possíveis.

No caso da moeda representamos o seu espaço amostral por: S = {cara, coroa}

Então pela formula de acontecer cara é:

P(cara) =  1/2   0,5  ou 50 %

Agora vamos as análises e conclusões:

Isso pode ser traduzido enganosamente como: terei um resultado cara a cada dois lances. Mas não é tão simples assim. Se você espera cara e, no primeiro lance, você obteve coroa, o lance seguinte tende a resultar em cara?   NÃO. 
Dizemos que os lances sucessivos são independentes, o que significa que a cada lance o cálculo deve ser refeito. 
Se no primeiro lance deu coroa, no segundo, a probabilidade de obter cara continua sendo de 1/2. Esse número significa que, após a observação de um número imenso de lances (um número que tende ao infinito), você terá aproximadamente a mesma quantidade de resultados cara e de resultados coroa.
É por isso que a teoria das probabilidades é conhecida como teoria dos grandes números, no máximo, podemos dizer que essa teoria sugere que, se você apostar um número muito grande de vezes nesse jogo, você tende a ganhar em 50% dos casos e perder nos outros 50%.

Transpassando isso para os jogos de loterias:

Algumas pessoas, quando apostam na loto, observam os últimos sorteios e constatam que há um conjunto de números que ocorreu poucas vezes, ou nenhuma vez. Se a probabilidade diz que todos os números tem as mesmas chances de serem sorteados, essa pessoa conclui que no próximo sorteio, esses números têm maiores chances de ocorrer. Essa ideia é equivocada, pois cada sorteio é independente, e a probabilidade de cada número ser sorteado continua sendo a mesma do dia em que a loto foi inventada.   

Se quisermos saber as probabilidades de tirarmos cara duas vezes, em dois lances consecutivos, as probabilidades se multiplicam ("multiplicar" aqui não tem nada a ver com "obter um número maior", pois estamos multiplicando frações). Então, se quero ter cara em dois lances, o cálculo é 1/2 x 1/2 = 1/4 ou 25%. Cara em três lances: 1/2 x 1/2 x 1/2 = 1/8 ou 12,5%.  

Se o jogo consiste em obter o resultado cara, pelo menos uma vez, lançando simultaneamente 2 moedas podemos ter a ilusão de que as probabilidades se somam: 50% para uma moeda + 50% para outra = 100%. Isso está errado! Para efetuar esse cálculo, é preciso voltar à definição básica de probabilidade: o número de casos favoráveis dividido pelo número de casos possíveis.

Quais são os casos possíveis no lançamento de duas moedas (chamaremos cada uma de moeda A e moeda B):  

1) cara na moeda A e cara na moeda B (favorável)  
2) cara na moeda A e coroa na moeda B (favorável)  
3) coroa na moeda A e cara na moeda B (favorável)  
4) coroa na moeda A e coroa na moeda B (não favorável)  

Temos 3 casos favoráveis dentro de 4 casos possíveis. Ou seja, a probabilidade em questão é de 3/4 ou 75%.

As probabilidades nos jogos:

Há ainda um outro dado a ser considerado, no caso das loterias, bingos, jogos de cassinos e coisas do gênero. Eles são feitos de tal forma que a probabilidade de o jogador ganhar é menor do que a de perder. Vejamos, a esse respeito, algumas considerações: 

"O prazer de se entregar aos jogos do puro acaso, oscila entre a vertigem do desconhecido e o cálculo de combinações sutis, entre a subjetividade humana e a ciência exata das estatísticas. O jogador tem prazer em elaborar suas combinações originais. Ele desafia as leis do destino, ele sabe convenientemente que, se as probabilidades de ganhar são pequenas, há sempre essa possibilidade mágica de faturar o grande prêmio e, assim, se tornar rico instantaneamente, sem esforço!

Com sorte, o feliz evento ocorre, mesmo que suas probabilidades de realização sejam pequenas".   

Isso exprime bem as motivações que muitos tem para apostar seu dinheiro na esperança de ficar rico, mas observemos os organizadores e administradores das loterias representam a única parte que sempre sai ganhando, isso porque os jogos de loterias são complexamente montados por matemáticos a favor dos organizadores.

Agora se você leu esse texto até aqui pode estar decepcionado pois a realidade dos números é um pouco mais cruel do que imaginava, mas não desanime tão fácil, pois iremos usar algumas técnicas e estratégias a favor dos que gostam de testar sua sorte em jogos e aumentando suas chances de vitória.

Vamos frequentemente ir dando algumas dicas valiosas. 1ª dica do blog...,

Participe de um bolão:

Monte um grupo em seu escritório, escola, igreja, centro de atividades ou qualquer outro lugar aonde outras pessoas queiram jogar na loteria com você. Ou, você pode comprar uma cota pronta em um bolão feito pela própria lotérica aonde você faz suas apostas, junto de pequena taxa administrativa extra, é claro.

O prêmio que você receberá será menor por causa da divisão, mas suas chances de vencer aumentam significantemente.