Probabilidade com jogo de cartas e o diagrama de Venn

Seriado Numb3rs -

Numb3rs é um show televisivo americano produzido pelos irmãos Ridley Scott e Tony Scott. Criada por NicolasFalacci e Cheryl Heuton, foi produzida pela Rede de Televisão Paramount/CBS e levada ao ar pela rede CBS nos Estados Unidos

https://pt.wikipedia.org/wiki/Numb3rs

Recentemente colegas de faculdade tiveram a brilhante ideia de compartilhar um episodio dessa serie da TV americana com os alunos na sala de aula, para quem já conhece a serie é bom rever, quem não conhece abaixo algumas detalhes desse programa aonde cada capitulo traz um conceito do universo matemático, assim que os "magos" desse blog encontrar qual episodio aborda um foco em probabilidades vamos atualizar a informação aqui.

---

Numb3rs (que se pronuncia Numbers) é uma série policial de televisão produzida pelos irmãos Ridley e Tony Scott e criado por Nicolas Falacci e Cheryl Heuton, através da CBS Paramount Network Television e apresentada originalmente nos Estados Unidos pela CBS, a partir de 23 de janeiro de 2005.

O espetáculo se encontrava em produção até o fechamento desta matéria em abril de 2010, com cerca de 118 episódios produzidos, de aproximadamente 43 minutos cada, em seis temporadas e no Brasil através da televisão a cabo A&E.

O seriado narra o cotidiano do Agente Federal do FBI chamado Don Eppes, interpretado por Rob Morrow e seu irmão, um gênio da matemática, Charlie Eppes protagonizado por David Krumholtz, que ajuda o seu irmão Don a resolver diversos crimes para o FBI.

Os acontecimentos e as relações entre Don, seu irmão Charlie e também com pai deles, Alan Eppes se passam na cidade de Los Angeles. O espetáculo tem como característica mostrar um episódio típico que tem início num crime, que passa a serem investigados pela equipe de agentes da FBI, liderados por Don e analisados matematicamente por Charlie.

Os dois geralmente também recebem auxílio de Larry Fleinhardt  e/ou Amita Ramanujan. Os dados matemáticos fornecidos pelo irmão Charlie, normalmente são o ponto crucial para a resolução dos crimes.

Apesar do seriado ser um grande sucesso, alguns matemáticos expressam preocupação com o uso da matemática e seus jargões soando como plausível, em lugar de ter consultores reais envolvidos em todas as fases do desenvolvimento da história.

Outros críticos também incluem aspectos impróprios na relação entre Charlie Eppes e a estudante Amita Ramanujan. Os criadores da série, Nicolas Falacci e Cheryl Heuton ganharam vários prêmios com o espetáculo, inclusive a Carl Sagan Award para “Public Understanding of Science” em 2006 e o “National Science Board´s Public Service Award”, em 2007.

Também o coordenador do espetáculo, Jim Vickers foi indicado para o Emmy Awards por “Outstanding Stunt Coordination” em 2006, pelo episódio da segunda temporada, “Harvest”.

Elenco

Rob Morrow como Don Eppes

David Krumholtz como Charlie Eppes

Judd Hirsch como Alan Eppes

Alimi Ballard como David Sinclair

Dylan Bruno como Colby Granger

Peter MacNicol como Dr. Larry Fleinhardt

Navi Rawat como Amita Ramanujan

Aya Sumika como Liz Warner

Diane Farr como Megan Reeves

Sabrina Lloyd como Terry Lake

Episódios

Primeira Temporada

1 - Pilot
2 - Uncertainty Principle
3 - Vector
4 - Structural Corruption
5 - Prime Suspect
6 - Sabotage
7 - Counterfeit Reality
8 - Identity Crisis
9 - Sniper Zero
10 - Dirty Bomb
11 - Sacrifice
12 - Noisy Edge
13 - Manhunt

Segunda Temporada

14 - Judgment Call
15 - Better Or Worse
16 - Obsession
17 - Calculated Risk
18 - Assassin
19 - Soft Target
20 - Convergence
21 - In Plain Sight
22 - Toxin
23 - Bones Of Contention
24 - Scorched
25 - The O.G.
26 - Double Down
27 - Harvest
28 - The Running Man
29 - Protest
30 - Mind Games
31 - All's Fair
32 - Dark Matter
33 - Guns and Roses
34 - Rampage
35 - Backscatter
36 - Undercurrents
37 - Hot Shot

Terceira Temporada

38 - Spree (1)
39 - Two Daughters (2)
40 - Provenance
41 - The Mole
42 - Traffic
43 - Longshot
44 - Blackout
45 - Hardball
46 - Waste Not
47 - Brutus
48 - Killer Chat
49 - Nine Wives
50 - Finders Keepers
51 - Take Out
52 - End Of Watch
53 - Contenders
54 - One Hour
55 - Democracy
56 - Pandora's Box
57 - Burn Rate
58 - The Art Of Reckoning
59 - Under Pressure
60 - Money For Nothing
61 - The Janus List

Quarta Temporada

62 - Trust Metric
63 - Hollywood Homicide
64 - Velocity
65 - Thirteen
66 - Robin Hood
67 - In Security
68 - Primacy
69 - Tabu
70 - Graphic
71 - Chinese Box
72 - Breaking Point
73 - Power
74 - Black Swan
75 - Checkmate
76 - End Game
77 - Atomic No. 33
78 - Pay to Play
79 - When World's Collide

Quinta Temporada

80 - High Exposure
81 - Decoy Effect
82 - Blowback
83 - Jack of All Trades
84 - Scan Man
85 - Magic Show
86 - Charlie Don't Surf
87 - Thirty Six Hours
88 - Conspiracy Theory
89 - Frienemies
90 - Arrow of Time
91 - Jacked
92 - Trouble in Chinatown
93 - Sneakerhead
94 - Guilt Trip
95 - Cover Me
96 - First Law
97 - 12:01 A.M.
98 - Animal Rites
99 - The Fifth Man
100 - Disturbed
101 - Greatest Hits
102 - Angels and Devils

Sexta Temporada

103 - Hangman
104 - Friendly Fire
105 - 7 Men Out
106 - Where Credit's Due
107 - Hydra
108 - Dreamland
109 - Shadow Markets
110 - Ultimatum
111 - Con Job
112 - Old Soldiers
113 - Scratch
114 - Arm in Arms
115 - Devil Girl
116 - And The Winner Is...
117 - Growin' Up
118 - 12 de Março de 2010 - Cause and Effect

Ainda em produção

Fórmula Básica da Probabilidade.

Fórmula Básica da Probabilidade de ocorrer um Evento.

Pascal descreveu a fórmula da probabilidade de um evento E como sendo:

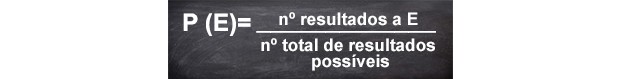
Traduzindo a fórmula, a probabilidade de um evento ocorrer é o numero de casos favoráveis dividido pelo numero de casos possíveis.

Veja um exemplo simples: Uma moeda “honesta” é lançada. 
Qual é a probabilidade de sair 1 cara ou 1 coroa?

Representamos um espaço amostral, pela letra S, esse é o total de 
casos possíveis.

No caso da moeda representamos o seu espaço amostral por: S = {cara, coroa}

Então pela formula de acontecer cara é:

P(cara) =  1/2   0,5  ou 50 %

Agora vamos as análises e conclusões:

Isso pode ser traduzido enganosamente como: terei um resultado cara a cada dois lances. Mas não é tão simples assim. Se você espera cara e, no primeiro lance, você obteve coroa, o lance seguinte tende a resultar em cara?   NÃO. 
Dizemos que os lances sucessivos são independentes, o que significa que a cada lance o cálculo deve ser refeito. 
Se no primeiro lance deu coroa, no segundo, a probabilidade de obter cara continua sendo de 1/2. Esse número significa que, após a observação de um número imenso de lances (um número que tende ao infinito), você terá aproximadamente a mesma quantidade de resultados cara e de resultados coroa.
É por isso que a teoria das probabilidades é conhecida como teoria dos grandes números, no máximo, podemos dizer que essa teoria sugere que, se você apostar um número muito grande de vezes nesse jogo, você tende a ganhar em 50% dos casos e perder nos outros 50%.

Transpassando isso para os jogos de loterias:

Algumas pessoas, quando apostam na loto, observam os últimos sorteios e constatam que há um conjunto de números que ocorreu poucas vezes, ou nenhuma vez. Se a probabilidade diz que todos os números tem as mesmas chances de serem sorteados, essa pessoa conclui que no próximo sorteio, esses números têm maiores chances de ocorrer. Essa ideia é equivocada, pois cada sorteio é independente, e a probabilidade de cada número ser sorteado continua sendo a mesma do dia em que a loto foi inventada.   

Se quisermos saber as probabilidades de tirarmos cara duas vezes, em dois lances consecutivos, as probabilidades se multiplicam ("multiplicar" aqui não tem nada a ver com "obter um número maior", pois estamos multiplicando frações). Então, se quero ter cara em dois lances, o cálculo é 1/2 x 1/2 = 1/4 ou 25%. Cara em três lances: 1/2 x 1/2 x 1/2 = 1/8 ou 12,5%.  

Se o jogo consiste em obter o resultado cara, pelo menos uma vez, lançando simultaneamente 2 moedas podemos ter a ilusão de que as probabilidades se somam: 50% para uma moeda + 50% para outra = 100%. Isso está errado! Para efetuar esse cálculo, é preciso voltar à definição básica de probabilidade: o número de casos favoráveis dividido pelo número de casos possíveis.

Quais são os casos possíveis no lançamento de duas moedas (chamaremos cada uma de moeda A e moeda B):  

1) cara na moeda A e cara na moeda B (favorável)  
2) cara na moeda A e coroa na moeda B (favorável)  
3) coroa na moeda A e cara na moeda B (favorável)  
4) coroa na moeda A e coroa na moeda B (não favorável)  

Temos 3 casos favoráveis dentro de 4 casos possíveis. Ou seja, a probabilidade em questão é de 3/4 ou 75%.

As probabilidades nos jogos:

Há ainda um outro dado a ser considerado, no caso das loterias, bingos, jogos de cassinos e coisas do gênero. Eles são feitos de tal forma que a probabilidade de o jogador ganhar é menor do que a de perder. Vejamos, a esse respeito, algumas considerações: 

"O prazer de se entregar aos jogos do puro acaso, oscila entre a vertigem do desconhecido e o cálculo de combinações sutis, entre a subjetividade humana e a ciência exata das estatísticas. O jogador tem prazer em elaborar suas combinações originais. Ele desafia as leis do destino, ele sabe convenientemente que, se as probabilidades de ganhar são pequenas, há sempre essa possibilidade mágica de faturar o grande prêmio e, assim, se tornar rico instantaneamente, sem esforço!

Com sorte, o feliz evento ocorre, mesmo que suas probabilidades de realização sejam pequenas".   

Isso exprime bem as motivações que muitos tem para apostar seu dinheiro na esperança de ficar rico, mas observemos os organizadores e administradores das loterias representam a única parte que sempre sai ganhando, isso porque os jogos de loterias são complexamente montados por matemáticos a favor dos organizadores.

Agora se você leu esse texto até aqui pode estar decepcionado pois a realidade dos números é um pouco mais cruel do que imaginava, mas não desanime tão fácil, pois iremos usar algumas técnicas e estratégias a favor dos que gostam de testar sua sorte em jogos e aumentando suas chances de vitória.

Vamos frequentemente ir dando algumas dicas valiosas. 1ª dica do blog...,

Participe de um bolão:

Monte um grupo em seu escritório, escola, igreja, centro de atividades ou qualquer outro lugar aonde outras pessoas queiram jogar na loteria com você. Ou, você pode comprar uma cota pronta em um bolão feito pela própria lotérica aonde você faz suas apostas, junto de pequena taxa administrativa extra, é claro.

O prêmio que você receberá será menor por causa da divisão, mas suas chances de vencer aumentam significantemente.

Introdução e definição de Probabilidade

A palavra probabilidade deriva do Latim probare (provar ou testar). Informalmente, provável é uma das muitas palavras utilizadas para eventos incertos ou desconhecidos , sendo também substituída por algumas palavras como “sorte”, “risco”, “azar”, "chance", “incerteza”, “duvidoso”, dependendo do contexto.

O surgimento da probabilidade está fundamentado em relatos históricos relacionados à disseminação dos jogos de azar na Idade Média, o qual era praticado envolvendo apostas. 
Os italianos Gerônimo Cardano (1501 – 1576), Galileu Galilei (1564 – 1642), Luca Pacioli (1445 – 1517) e Niccolo Tartaglia (1499 – 1557) foram os matemáticos responsáveis pelo desenvolvimento das primeiras teorias envolvendo jogos e apostas. Eles deram início aos estudos envolvendo o jogo de dados, trabalhando as ideias do conjunto universo e dos eventos pertencentes a este conjunto. 

O interesse por situações mais complexas fez com que outros matemáticos aprofundassem os estudos no intuito de estabelecer novas teorias. Entre os mais importantes podemos citar: 

Blaise Pascal (1623 – 1662) 
Pierre de Fermat (1601 – 1655) 
Christiaan Huygens (1629 – 1695) 
Jacob Bernoulli (1654 – 1705) 
Pierre Simon Laplace (1749 – 1827) 
Carl Friedrich Gauss (1777 – 1855) 
Lenis Poisson (1781 – 1840) 
Abraham de Moivre (1667 – 1754) 
Pafnuti Tchebycheff (1821 – 1894) 
Andrei Andreyevitch Markov (1856 – 1922) 
Andrei Nikolaevich Kolmogorov (1903 – 1987) 

Pascal e Fermat foram os responsáveis por estabelecer as bases da teoria do cálculo probabilístico e inúmeras hipóteses foram levantadas envolvendo possíveis resultados, marcando o início da teoria das probabilidades como ciência. A abordagem de Bernoulli envolveu os grandes números, surgindo as combinações, permutações e classificação binomial. A contribuição de Laplace foi através da regra de sucessão e Gauss estabeleceu o método dos mínimos quadrados e a lei das distribuições. 

Atualmente, o estudo das teorias probabilísticas é de grande importância, em virtude de seus axiomas, teorema e definições incisivas. Possui aplicação nos estudos relacionados à estatística, economia, engenharia, física, química, jogos estratégicos, sociologia, psicologia, biologia, entre outros ramos do conhecimento.